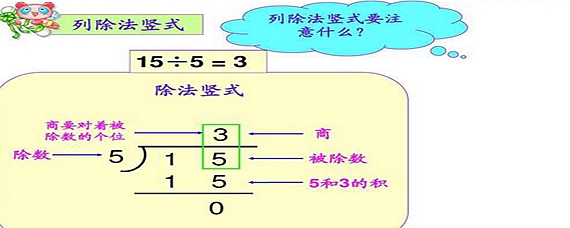
除法竖式计算方法包括以下步骤:,1. 确定被除数和除数,将被除数写在除法竖式的上方,除数写在左侧。,2. 计算商的位数,即被除数最高位除以除数的结果,将商写在被除数的上方。,3. 计算余数,即将被除数减去商与除数的乘积,将余数写在被除数的下方。,4. 将余数与被除数的下一位数组合成新的被除数,重复上述步骤,直到余数为0或被除数已经全部用完。,5. 如果余数为0,则商已经全部计算完毕;如果余数不为0,则需要在商的末尾添加相应的0,并继续计算下一位的商。,6. 最终得到的商就是除法竖式的计算结果。
在小学数学中,除法是一个基础且重要的概念,它不仅关乎日常生活的应用,也是后续学习更复杂数学概念的基础,掌握除法竖式的计算方法,对于学生来说至关重要,本文将详细介绍除法竖式的计算步骤,通过图文并茂的方式,帮助读者更好地理解和掌握这一技能。
除法竖式的基本概念
除法竖式是一种直观的、逐步进行的除法计算方法,它通过将除数(被除数)与除数进行逐位比较,并逐步减去商与除数的乘积,直到余数小于除数为止,这种方法不仅适用于手算,也广泛应用于笔算和电子计算中。
除法竖式的计算步骤
步骤1:确定商的位置
- 将除数(通常为较小的数)写在被除数(通常为较大的数)的左侧,并确定商的起始位置,商的起始位置从被除数的最高位开始。
- 计算1234 ÷ 56时,56写在1234的左侧,商的起始位置为1(即从百位开始)。
步骤2:逐位相除
- 从被除数的最高位开始,用除数去除该位及其以下的所有位数,如果该位小于除数,则商为0;如果大于或等于除数,则商为该位上的数字。
- 继续用上一步得到的商与除数的乘积从被除数中减去,得到新的余数。
- 重复上述过程,直到余数小于除数为止。
步骤3:处理余数
- 如果在某一步中余数小于除数,则该步骤的商即为最终结果;如果余数仍然大于或等于除数,则继续用下一个更高位的数字作为新的商的起始部分,重复上述过程。
- 需要注意的是,如果被除数的位数少于除数的位数(即“不够除”),则直接在商的相应位置写0。
具体示例解析
示例1:计算1234 ÷ 56
-
确定商的位置:从百位开始,即商的起始位置为1。
| | 1 | 2 | 3 | 4 | | | | | | | | | | | | 56 | | | | | | | 1 | 2 | 3 | 4 | 余数 |
-
逐位相除:用56去除12(百位),商为2(因为12 ≥ 56),然后减去112(2 × 56),得到余数14。
| | 2 | 2 | 3 | 4 | | | | | | | | | | | | 56 | 112 | 14 | 余数 |
-
继续相除:用56去除140(十位及以下),商为2(因为140 ≥ 56),然后减去112,得到余数28。
| | 2 | 2 | 2 | 8 | | | | | | | | | | | | 56 | 112 | 28 | 余数 |
-
最后相除:用56去除28(个位),商为0(因为28 < 56),然后减去0,得到余数28,由于余数不再变化且小于除数,所以最终结果为:1234 ÷ 56 = 22.046...(保留四位小数),但在此竖式计算中,我们只进行到余数小于除数为止的步骤。
示例2:计算789 ÷ 99
由于789的位数少于99的位数,直接在商的最高位写0,然后从个位开始计算:
-
确定商的位置:从个位开始,即商的起始位置为0,但因为不够除,所以直接写0。
| | 0 | 7 | 8 | 9 | | | | | 99 | 余数 |
-
逐位相除:用99去除78(个位及以下),由于78 < 99,所以商为0,余数为78,然后继续用下一个数字(即7)作为新的被除数的最高位,但此时因为7 < 99且没有更多位数可加,所以直接在商的十位写0,最终结果为:789 ÷ 99 = 0.79...(保留一位小数),但同样地,我们在此竖式计算中只进行到无法再继续为止的步骤。
注意事项与常见错误
- 确保每次减法后余数小于除数:这是进行下一步的前提条件,如果余数大于或等于除数,则需继续用下一个更高位的数字作为新的被除数的最高位进行计算。
- 避免“假借位”:在计算过程中不要随意“借位”或“进位”,这会导致结果不准确,每次借位或进位都应基于实际的减法操作和余数的比较结果。
- 细心观察和计算:在逐位相减时,要细心观察每一步的结果是否正确,特别是当遇到连续的0时(如上例中的“078”),要确保不会误读或误写。
- 熟练掌握乘法表:在进行乘法和减法时,熟练掌握乘法表可以大大提高计算速度和准确性,知道56 × 2 = 112等基本乘法结果可以快速完成减法操作。
- 理解概念本质:最重要的是理解除法竖式的本质——逐步减少被除数的值直到无法再减为止的过程,这有助于在遇到复杂问题时能够灵活应对和解决。

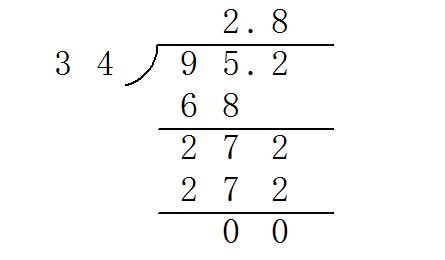
 京公网安备11000000000001号
京公网安备11000000000001号 浙ICP备11054653号-2
浙ICP备11054653号-2