除法竖式计算题是数学中一项基础而重要的技能，它不仅能帮助我们理解分数的概念，还能在解决实际问题时提供关键工具，通过将被除数按照除数的位置逐一分配，我们可以直观地看到每次分配后剩余的部分，从而得出商和余数，这一过程不仅锻炼了我们的数学思维能力，还培养了我们对数字的敏感性和精确度，掌握除法竖式计算，就如同掌握了一把解锁数学奥秘的钥匙，让我们在解决复杂问题时更加游刃有余。

在数学的浩瀚海洋中，除法作为基础运算之一，其重要性不言而喻，它不仅是日常生活解决分配问题的重要工具，也是学习更复杂数学概念如分数、小数和代数的基础，而通过除法竖式这一直观的呈现方式，我们能够更清晰地理解除法运算的每一步，从而在解决实际问题时游刃有余，本文将深入探讨除法竖式的计算方法，通过实例解析，帮助读者掌握这一技能,开启数学世界的新大门。

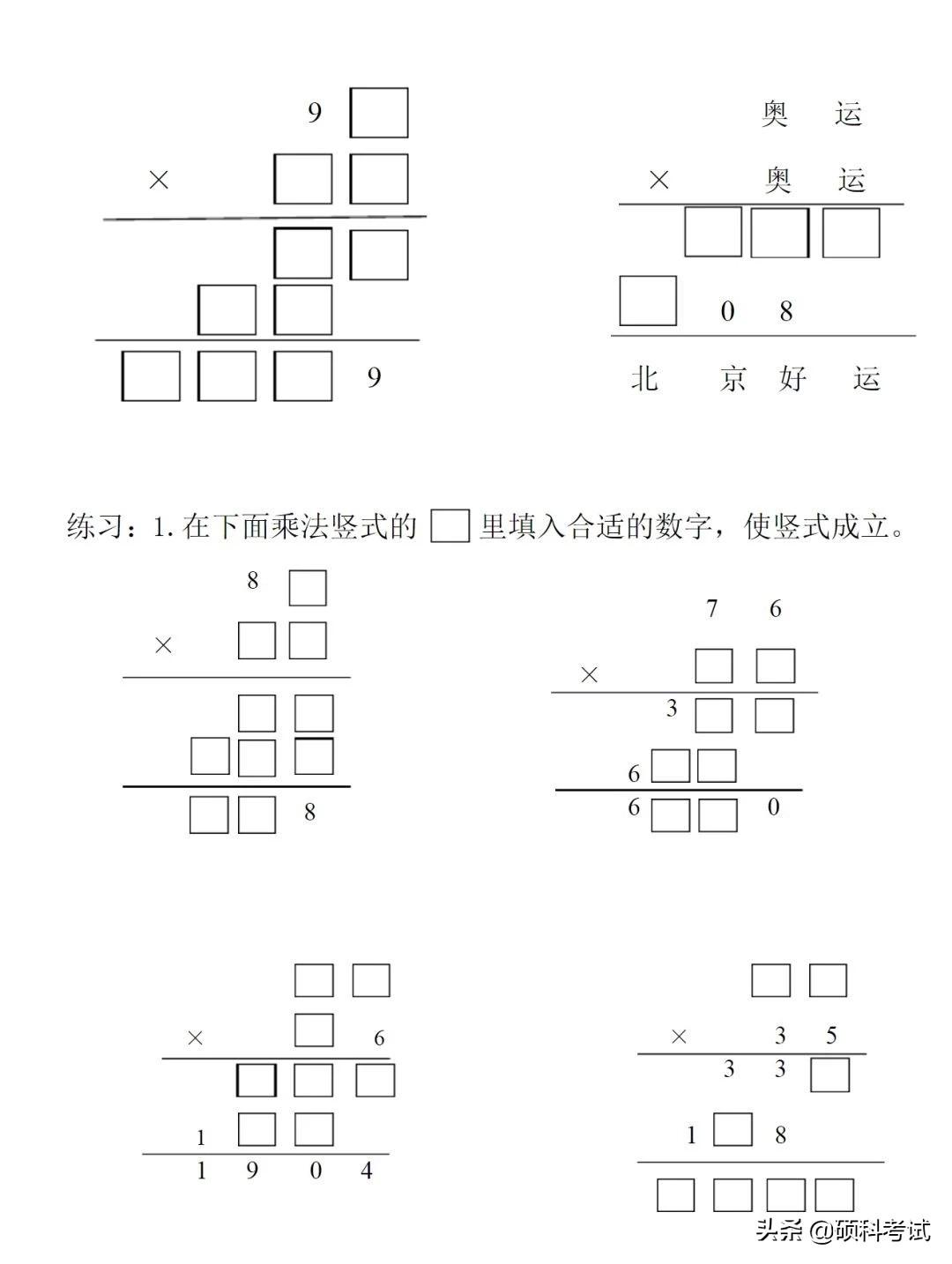
除法竖式的基本概念

除法竖式是一种将除法运算过程以直观、分步的形式展现出来的计算方法，它包括被除数、除数、商和余数四个基本元素，在竖式计算中，我们从左至右逐位进行除法操作，每一步都基于前一步的结果,确保了计算的准确性和可追溯性。

除法竖式的步骤解析

1. 确定商的位置：我们将除数与被除数的最高位进行除法运算，以确定商的最高位数字，这一步的关键是理解“看被除数的前几位能够被除数整除”。

   

2. 计算商的每一位：在确定了商的最高位后，我们将该位与除数相乘，并将结果写在被除数的下方，用被除数减去这个乘积，得到的结果即为新的余数，我们再对被除数的下一位进行同样的操作,重复此过程直到被除数被完全除尽或达到所需的精度。

3. 处理余数：如果最终仍有余数且不等于0（且题目无特别要求继续除），则该余数即为最终结果；若题目要求继续除（如求小数形式），则需将余数与被除数的下一位（或0）组合,继续上述过程直至满足条件。

实例解析：用除法竖式解决实际问题

例1：计算72 ÷ 9

• 步骤一：确定商的最高位，72的十位7能被9整除，所以商的十位为0（实际上此处为7/9的近似处理，但为简化说明，我们直接取整）。
• 步骤二：计算7（被除数十位）除以9，商为0，写于十位下方；然后9乘以0得0,从72中减去0后得到72作为新的被除数。
• 步骤三：接下来是72的个位2，由于2小于9无法直接除尽，我们通常采用“补零”策略（即视为20），但这里为了保持示例的简洁性，我们直接处理个位2,在正式计算中应将2视为20的一部分来处理。
• 步骤四：将2除以9得0余2，即商的个位为0，余数为2，72 ÷ 9 = 8……2（若考虑补零策略则更精确）。

例2：计算153 ÷ 11

• 步骤一：确定商的最高位，153的百位1能被11整除的次数为0次（即11*0=0），所以商的百位为0，接着考虑15（十位和个位），由于15小于11无法直接除尽，我们采用“补零”策略,视作150来处理。
• 步骤二：用150除以11得13余7（注意这里已通过补零将问题简化），将商13写于百位下方；然后11乘以13得143,从153中减去143得0作为新的余数。
• 步骤三：由于已无剩余位数且余数为0，所以计算结束，153 ÷ 11 = 14……0（实际补零后计算）。

注意事项与技巧

• 补零技巧：当某一位上的数字小于除数时，可以通过在前面补零来使其达到可除的程度,这有助于简化计算过程并提高准确性。
• 验算：完成计算后，通过乘法验算（即商乘以除数加余数）可以检查答案的正确性。
• 耐心与细心：由于竖式计算涉及多个步骤和细节处理,因此需要耐心和细心地对待每一环节。
• 理解概念：最重要的是理解每一步背后的数学原理和逻辑关系,这样才能真正掌握除法竖式的精髓。

教育意义与应用价值

学习除法竖式不仅是为了解决数学问题本身，更是为了培养逻辑思维、精确计算和问题解决的能力，在日常生活和科学研究中，这些能力是不可或缺的，在财务管理中计算分摊费用、在烹饪时按比例分配食材、在工程设计时根据需求分配资源等场景中，除法都扮演着重要角色，它还是进一步学习更高级数学概念如代数、微积分等的基础。

除法竖式计算题是通往数学殿堂的一把钥匙，通过不断的练习和深入理解，我们不仅能够熟练掌握这一技能，还能在解决实际问题的过程中展现出强大的数学素养和逻辑思维能力,让我们以耐心和热情去探索数学的奥秘吧！